| |
| ||
       |
 |
 |
|
|
 |
 |
 |
|
 | |||
| |||||
|
|
Этот Документ | | ||
|
|
| |||
| |||||
|
|
 |
SummaryPlus | |
|
|
|
 |
Полный Текст + Ссылки | |
|
|
|
Изображения Размера ·Full | |
| |
|
|
|
PDF (640 K) | |
|
|
|
| |||
| |||||
|
|
| |||
|
|
Действия | | ||
|
|
| |||
| |||||
|
|
|
Процитированный | | |
|
|
|
Сохраните как Предупреждение Цитаты | | |
|
|
|
Почтовая Статья | | |
|
|
|
Экспортная Цитата | | |
 |
|
 | |||
| |||||
Аналитическое моделирование приближается для сети, направляющей алгоритмы, которые используют "подобные муравью" мобильные вещества
Найджел Beana и Andre Costaa, b
, 
Математика aApplied, Университет Аделаиды, Аделаиды 5005, Австралия
bCentre Превосходства для Математики и Статистики Сложных Систем, Университета Мельбурна, Мельбурна 3010, Австралия
Полученный 23 мая 2004; пересмотренный 20 октября 2004; принятый 10 января 2005. Ответственный Редактор: F. Cuomo. Доступный онлайн 22 февраля 2005.
В этой газете мы вводим аналитический подход моделирования к исследованию нового класса адаптивной сети, направляющей алгоритм, который вдохновлен решающими проблему поведениями на стадии становления, наблюдаемыми в биологических колониях муравьев. Этот класс алгоритма использует "подобных муравью" агентов, которые пересекают сеть и все вместе создают политику маршрутизации. Предыдущие исследования сосредоточились исключительно на экспериментах моделирования, которые указывают, что такие алгоритмы выступают хорошо в ответ на изменения в реальном времени в запросах трафика и сетевых условиях. Аналитическая модель, представленная в этой газете, разрешает полезную способность проникновения в суть определенных фундаментальных аспектов основанных на муравье алгоритмов, которые не были обсуждены в предыдущей основанной на муравье литературе маршрутизации. В частности работа, представленная в этой газете, мотивирует наше предложение многих модификаций к базовой конструкции основанных на муравье алгоритмов маршрутизации, которые приводят к улучшенной работе относительно критериев качества работы равновесия.
Ключевые слова: Адаптивная маршрутизация; Основанная на муравье маршрутизация; Укрепление, учащееся; равновесие Wardrop
Со дней самых ранних распределенных компьютерных сетей, через к современному Интернету, интерес в адаптивных и децентрализованных системах для того, чтобы направить управление в сетях управлял развитием алгоритмов, которые стремятся динамически реконфигурировать трафик, направляющий политику, в ответ на изменения в реальном времени в запросах трафика и сетевых условиях. Примеры колеблются от Распределенной Bellman–Ford Algorithm [1], к более свежим схемам маршрутизации, основанным на изучении укрепления и стохастической оптимизации [2], [3], [4] и [5].
В пределах этого контекста интересный и новый вклад произошел от недавно развитой и известной стохастической оптимизации, мета-эвристической известный как Оптимизация Колонии муравьев [6] и [7], который берет ее вдохновение от коллективных решающих проблему поведений, наблюдаемых в биологических колониях муравьев. Приложение этого мета-эвристического к проблеме адаптивной маршрутизации и балансирования загрузки в системах коммуникаций привело к развитию многих динамических алгоритмов маршрутизации, которые нанимают "подобных муравью" мобильных агентов [8], [9], [10], [11] и [12]. Эти алгоритмы, известные как основанные на муравье алгоритмы маршрутизации, пытаются воспроизвести в искусственной системе некоторые из коллективных способностей решения задач, которые экстенсивно наблюдались и зарегистрированы в биологическую копию (см. [6] для примеров и справочной информации).
Как отмечено в недавней газете обзора [13], исследование, выполненное в области основанных на муравье алгоритмов маршрутизации, было пока ограничено основанному на моделировании моделированию и анализу. Наиболее особенно, исследования моделирования, представленные в [9], указывают, что основанные на муравье алгоритмы маршрутизации выступают хорошо когда сравнено со стандартными алгоритмами маршрутизации в настоящее время, используемыми в Интернете, такими как Распределенный Форд глашатая [1] и OSPF [14], которые типично используются вместе с самым коротким путем, направляющим [1]. Центр таких исследований моделирования был на переходных мерах работы в ответ на внезапные изменения в запросах трафика и сетевых условиях [9]. В то время как такие рассмотрения очень важны для исследования любого адаптивного алгоритма маршрутизации, мы показываем в этой газете, что много полезной информации и способности проникновения в суть может быть получено от исследования равновесия (установившиеся) свойства основанных на муравье алгоритмов маршрутизации. В частности мы представляем аналитический подход моделирования для исследования основанных на муравье алгоритмов маршрутизации, которое служит, чтобы привлечь внимание ко многим теоретическим аспектам, которые не были сделаны с готовностью очевидными через основанное на моделировании исследование, выполненное до настоящего времени.
Привлекая аспекты укрепления, учащегося [2], теория [15] игры и нелинейная оптимизация [16], мы идентифицируем многую неэффективность, которая является врожденной от текущего дизайна основанных на муравье алгоритмов маршрутизации. Определенно, мы подсвечиваем факт, что основанные на муравье алгоритмы маршрутизации на политике изучают алгоритмы [2], в смысле, что механизм для того, чтобы выполнить исследование альтернативных решений маршрутизации не является полностью отдельным от механизма, используемого, чтобы принять решения маршрутизации. Мы утверждаем, что это - нежелательный аспект основанных на муравье алгоритмов маршрутизации, и мы предлагаем простые модификации, которые делают основанный на муравье подход вне политики [2], в смысле, что механизмы для исследования и принятия решения полностью расцеплены, не ставя под угрозу ни одну из этих задач.
Кроме того, мы сравниваем политику маршрутизации, произведенную основанными на муравье алгоритмами маршрутизации с пользователем и системно-оптимальными понятиями маршрутизации. Способность проникновения в суть, полученная через этот анализ, принуждает нас предлагать изменения дизайну основанных на муравье алгоритмов маршрутизации, которые улучшают их работу относительно мер по равновесию сетевой задержки. В частности мы показываем той теме определенным модификациям, основанные на муравье алгоритмы маршрутизации в состоянии достигнуть типа оптимизированной пользователем маршрутизации, известной как равновесие Wardrop [17].
Важно, мы отмечаем, что модификации, которые мы предлагаем в этом бумажном дополнении, но не идут на компромисс, желательные особенности основанных на муравье алгоритмов маршрутизации, которые сделали их обращающийся к исследователям в области систем коммуникаций (и действительно более широкое научное сообщество [18]), эти являющиеся их переходными адаптивными свойствами, надежностью, и децентрализовали структуру.
Эта бумага организована следующим образом. Раздел 2 обеспечивает краткое введение в коллективный самый короткий путь, находящий поведения, наблюдаемые в биологических колониях муравьев, которые вдохновили развитие основанных на муравье алгоритмов маршрутизации для систем коммуникаций. Раздел 3 обеспечивает краткий обзор главных основанных на муравье алгоритмов маршрутизации, которые были предложены в литературе, и в Разделе 4, мы описываем основанный на муравье алгоритм для того, чтобы направить в connectionless сетях пакетной коммутации [1], который формирует основание для анализа, представленного в этой газете.
В Разделе 5, мы представляем аналитическую модель, которая фиксирует поведение равновесия и определенные переходные свойства алгоритма, описанного в Разделе 4. Наш анализ основанных на муравье алгоритмов маршрутизации через аналитическую модель представлен в двух частях.
Для первой части, в Разделе 6, мы рассматриваем особый случай, где нет никаких запросов трафика данных, помещенных в сеть. Этот контекст обеспечивает простое транспортное средство для того, что оно расследовало эффект, который свойство на политике имеет на способность муравьев точно узнать о сетевых задержках. Вторая часть нашего анализа представлена в Разделе 7, где мы рассматриваем обычный случай, куда запросы трафика данных помещены в сеть. В этом контексте мы в состоянии исследовать способность основанных на муравье алгоритмов выполнить балансирование загрузки трафика по многократным маршрутам.
Мы предлагаем и анализируем улучшенную версию вне политики основанного на муравье алгоритма маршрутизации в Разделе 8. Заключения и обсуждение следуют в Разделе 9.
Биологические муравьи обладают многими качествами, которые желательны в искусственных системах, с технической точки зрения [6]. Индивидуально они управляют использующими простыми правилами, в то время как все вместе они в состоянии сформировать сложные образцы как "решения" проблемы обнаружения источников пищи. Кроме того, муравьи функционируют большая часть времени без централизованного управления, что означает, что колония муравьев - разными способами распределенная система, выполняя децентрализованное вычисление.
Интересный эксперимент, выполненный в лаборатории, известен как эксперимент двойного моста [19]. Это служит, чтобы подсветить, как простые правила, сопровождаемые индивидуальными муравьями, в состоянии дать начало коллективному процессу "принятия решения". Относительно этого специфического эксперимента муравьи, как наблюдали, следовали за правилами, которые могут быть получены в итоге как:
• депозит муравьев (химический) феромон по приблизительно постоянной норме, как они едут, 1 и
• муравьи в состоянии обнаружить различия в концентрации феромона в их среде, и будет иметь тенденцию двигаться в руководство, где концентрация является самой высокой.
Кроме того, как во многих естественных системах, там существует немного степени случайного колебания. Это может заставить индивидуальных муравьев следовать за путем с более низким или даже нулевым уровнем концентрации феромона. Этот тип поведения упоминается как исследование. Кроме того, феромон испаряется или распадается по приблизительно постоянной норме, что означает, что следы должны получить непрерывное укрепление, чтобы остаться уже существующими.
В двойном эксперименте моста муравьям разрешают установить след феромона между их вложенным множеством и источником пищи. Препятствие тогда помещено в путь муравьев, таким способом, которым у муравьев есть выбор двух путей вокруг преграды, один из которых является в два раза длиннее, чем другим. Первоначально, нет никакого феромона или на длинном или на коротком пути, и поэтому у муравьев есть равные вероятности выбирания любого пути. Это приводит к приблизительно половине муравьев, первоначально выбирающих длинный путь и наполовину выбирающих короткий путь.
Теперь полагайте, что муравьи вносят феромон по приблизительно постоянной норме, путешествие на приблизительно той же самой скорости, и путешествие в обоих указаниях между источником пищи и вложенным множеством. В результате после данного промежутка времени, больше муравьев пересекло всю длину короткого пути, чем пересекли длину длинного пути. Это означает, что после данного промежутка времени, концентрация феромона на коротком пути выше чем концентрация на длинном пути. Положительный процесс обратной связи следует, посредством чего после некоторого времени, большинство муравьев берет короткий путь. Таким образом, муравьи все вместе приняли "решение", и важно, решение - ясно оптимальный.
Это - этот вид коллективного решающего проблему поведения, описанного выше этого, вдохновил попытку перевести основные особенности биологических муравьев на искусственных муравьев для использования в вычислительном решении задач, приводя к развитию Оптимизации Колонии муравьев, мета-эвристической [21].
Последующее приложение Оптимизации Колонии муравьев, мета-эвристической к системе коммуникаций, является весьма естественным, чтобы сделать. Таблица 1 список аналогии, сделанные между реальными и искусственными муравьями в приложении искусственных муравьев к маршрутизации в системах коммуникаций; реальные муравьи становятся пакетами информации, которые физически едут через сеть в подобной манере к регулярным пакетам. Концентрации феромона на отличных следах переводят к weightings для вероятностного выбора ссылки в сетевых узлах. Смещение феромона тогда переводит как увеличение весов, и испарение феромона переводит как decrementing веса.
Аналогии между биологическими и искусственными муравьями
Биологический Искусственный Муравьи Информационные пакеты Следы Сетевые ссылки Пересечения следа Сетевые узлы Химический феромон Вероятностные веса на следе для выбора ссылки Смещение феромона Приращение веса Испарение феромона Декремент веса
Кроме того, от технической перспективы, желательно увеличить искусственных муравьев с дополнительными особенностями, не охваченными биологическими муравьями, чтобы избежать определенных недостатков биологических систем муравья.
Например, считайте двойной эксперимент моста описанным выше. Положительная обратная связь, которая, как замечается, все более и более одобряет выбор более короткого пути, является по существу переходным эффектом, являясь результатом факта, что концентрация феромона увеличивается по более быстрой норме на коротком пути. В двойном эксперименте моста также найдено, что, как только устойчивая область феромона установлена на коротком пути, если более короткий путь становится доступным, то муравьи не всегда в состоянии переключиться на это, и продолжить вместо этого ехать на том же самом пути [19]. Это указывает, что положительный эффект обратной связи, одобряя короткий путь решительно зависит от начальных условий, в этом случае, начального отсутствия феромона на любом пути.
Этого эффекта застоя, описанного выше, можно было бы избежать, если бы муравьи так или иначе были в состоянии внести феромон в количестве, которое отражает длину пути, на котором они едут. Это обеспечило бы дополнительный механизм для отличительного укрепления концентрации феромона на путях различных длин, в манере, которая не будет решительно зависеть от начальных условий.
В проектировании искусственного основанного на муравье алгоритма может легко быть введен отличительный механизм награды, посредством чего вместо того, чтобы внести искусственный "феромон" по постоянной норме, искусственные муравьи вносят феромон в количествах, которые обратно пропорционально пропорциональны задержке, связанной с путями, на которых они едут. Это может быть достигнуто, программируя муравьев, чтобы эффективно вернуться той же дорогой, и внести феромон после того, как путь был закончен, и задержка пути известна.
Многие алгоритмы, которые используют подобные муравью вещества, были предложены в литературе [8], [9], [10], [11] и [12]. Они отличаются по их степени изощренности, и в деталях их выполнения. Однако, у всех есть вместе идея использовать мобильные подобные муравью вещества, которые автономно пересекают сеть и пытаются найти "хорошие" маршруты между данными парами узла адресата происхождения. Сетевая информация, которая собрана муравьями, тогда используется, чтобы адаптивно изменить трафик данных сети, направляющий политику, чтобы эксплуатировать лучшие маршруты, которые идентифицированы муравьями.
Основанные на муравье алгоритмы маршрутизации могут быть характеризованы следующим образом. В каждом узле сети поддержана таблица маршрутизации муравья. Такая таблица маршрутизации содержит, для каждого возможного узла адресата, ряд вероятностей маршрутизации, соответствующих каждой из уходящих ссылок узла.
Муравьи периодически создаются в каждом узле, и каждый муравей назначен на данный узел адресата. Муравей, отступающий от его узла происхождения, выбирает уходящую ссылку probabilistically, согласно вероятностям маршрутизации, содержавшимся в таблице маршрутизации муравья в происхождении, и этот процесс повторен в каждом промежуточном узле, пока узел адресата не достигнут. Муравей хранит в его памяти информацию о маршруте, которым это следовало, и связанное время поездки. Восстанавливая его выбранные шаги от адресата назад к происхождению, муравей в состоянии обновить вероятности маршрутизации в узлах, что это посетило. Обновления - функции измерений времени поездки, которые были сделаны муравьем на его оригинальной передовой поездке. Коллективный эффект этих обновлений предназначен, чтобы увеличить вероятность, что другие муравьи выбирают ссылки, которые лежат на маршрутах с низкими связанными временами поездки, и наоборот, уменьшить вероятность ссылок выбора, которые лежат на маршрутах с большими связанными временами поездки. Положительный процесс обратной связи поэтому следует, посредством чего большинство муравьев путешествует на маршрутах с низкими временами поездки, и у ссылок, которые лежат на таких маршрутах, есть большие связанные вероятности маршрутизации.
Одновременно, трафик данных, направляющий политику, определен как функция муравья, направляющего вероятности. Специфическая манера, в которой это сделано, изменяется от одного основанного на муравье алгоритма до другого, и зависит от того, ориентируется ли сеть на подключение или connectionless (см. [1]). Основанные на муравье алгоритмы, которые были проектированы для ориентируемых на подключение сетей [11] и [8], применяют детерминированные данные, направляющие политику, посредством чего подключения установлены, резервируя запасную способность (если доступный) на ссылках, у которых есть самый высокий связанный муравей, направляющий вероятности. Напротив, основанные на муравье алгоритмы, которые были проектированы для connectionless сетей [9] и [10], применяют рандомизированные данные, направляющие политику, посредством чего пакеты данных, более вероятно, будут направлены при уходящих ссылках, у которых есть самый высокий связанный муравей, направляющий вероятности.
И в ориентируемом на подключение и в connectionless сети, мы видим, что трафик данных, направляющий механизм, пытается эксплуатировать маршруты, у которых, как оценивают муравьи, есть низкая связанная задержка.
Мы отмечаем, что роль, которая запускает муравей, направляющий вероятности в основанном на муравье алгоритме маршрутизации, походит на роль химического феромона в биологических колониях муравьев. Таким образом, муравей, направляющий вероятности, служит средой, через которую муравьи могут косвенно сообщить и поделиться информацией о временах поездки, связанных с различными маршрутами.
Важная особенность, которая способствует способности всех основанных на муравье алгоритмов приспособиться к изменениям в сетевой окружающей среде, то, что они выполняют немного степени исследования сети.
В биологической колонии муравьев происходит исследование, потому что муравьи в состоянии иногда следовать за следами с более низкой концентрацией феромона, или возможно даже поехать в руководстве, в котором концентрация феромона - ноль. Потребность этого типа поведения в биологической колонии муравьев ясна; например, без исследования, у муравьев не было бы средств, чтобы обнаружить новые источники пищи, когда старые израсходованы, или найти альтернативные пути между вложенным множеством и источником пищи, если оригинальный путь больше не жизнеспособен.
В сетевом контексте исследование может быть характеризовано как "исследование" многих возможных маршрутов, чтобы получить информацию о них. Исследование - ясно необходимая особенность любого алгоритма маршрутизации, который должен "учиться" о сети, потому что у алгоритма должны быть некоторые средства для оценки или оценки задержек, связанных с альтернативными маршрутами, даже если они в настоящее время находятся не в использовании.
Точно так же в сети, в которой системные параметры могут измениться неочевидно, маршруты, которые первоначально высоко связали задержку, например, возможно, позже низко связали задержку. Механизм исследования поэтому требуется, для алгоритма, чтобы быть в состоянии постоянно исследовать и переоценить задержку, связанную с альтернативными маршрутами.
Во всех основанных на муравье алгоритмах маршрутизации, предложенных до настоящего времени, исследование достигнуто, вынуждая муравья, направляющего вероятности далеко от ноля, таким образом что у каждой уходящей ссылки (и следовательно каждого возможного маршрута) есть по крайней мере немного маленькой вероятности того, чтобы быть отобранным муравьем. В этой газете мы демонстрируем, что сетевая работа может пострадать, когда исследование выполнено в этой манере, и мы предлагаем модификацию дизайну основанных на муравье алгоритмов маршрутизации, который сохраняет способность выполнить исследование, не жертвуя работой.
Цель этой бумаги состоит в том, чтобы развить аналитический подход моделирования для исследования основанных на муравье алгоритмов маршрутизации, которые разрешат нам получать способность проникновения в суть их фундаментальных свойств. Чтобы сделать так, мы ограничиваем свое внимание моделированием простого основанного на муравье алгоритма маршрутизации для connectionless сетей.
Алгоритм, который мы рассматриваем, основан на AntNet [9], но содержит только свои фундаментальные особенности. Этот подход позволяет нам формулировать аналитическую модель алгоритма, представленного в Разделе 5, который является и послушным и широко представительным для основанных на муравье алгоритмов маршрутизации для connectionless сетей. В частности способность проникновения в суть получила использование аналитической модели и усовершенствований, которые мы предлагаем в этой газете, относятся к любому алгоритму маршрутизации, который нанимает подобных муравью мобильных агентов.
Рассмотрите сеть, состоящую из ряда 
узлов, связанных набором направленных .gif){kind=small}
ссылок. Мы предполагаем, что таково,.gif){kind=small}
что есть путь между любыми двумя узлами. Таким образом, сеть - связанный граф. Для каждого узла есть .gif){kind=small}
ссылки к некоторому подмножеству узлов.gif){kind=small}
, которые мы называем соседними узлами меня.
В каждом узле i, следующие значения поддержаны для каждого узла адресата d в “формате” таблицы поиска:
1. Ряд Q-значений, 2 Qijd, для всех соседних узлов.gif){kind=small}
, где Qijd составляет оценку задержки, или время поездки, связанное с путешествием из узла i к d использование уходящей ссылки (я, j).
2. Ряд муравья, направляющего вероятности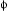 
ijd, для всех соседних узлов.gif){kind=small}
, где 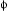ijd - вероятность, что муравей в узле i, с адресатом d, выбирает уходящую ссылку (я, j).
3. Ряд данных, направляющих вероятности ψijd, для всех соседних узлов.gif){kind=small}
, где ψijd - вероятность, что пакет данных в узле i, с адресатом d, направлен через уходящую ссылку (я, j).
Муравей и данные, направляющие вероятности, произведены согласно различным функциям оценок времен поездки, быть описанными коротко. Таким образом, муравьи и пакеты данных совместно используют ту же самую сеть, но направлены согласно различной "политике". Кроме того, муравьи активно измеряют времена поездки и кормят эту информацию назад в таблицы маршрутизации, обновляя оценки времени поездки, тогда как пакеты данных пассивно направлены через сеть согласно данным, направляющим вероятности.
Поведение и функциональные возможности муравьев следующие. Муравьи регулярно создаются во всех узлах и посылаются во все возможные узлы адресата. Каждому индивидуальному муравью поэтому назначают специфическая пара узла адресата происхождения. Муравей с узлом происхождения o и узлом адресата d пересекает сеть беспорядочно выбором уходящая ссылка в каждом посещаемом узле i согласно муравью, направляющему вероятности 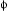ijd, пока узел адресата d не достигнут. В частности позвольте ik, k = 1, 2, … , N быть случайной последовательностью узлов, посещаемых муравьем, с i1 = o и в = d, где N 
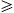2 является случайной переменной, обозначающей число узлов, включающих траекторию муравья.
Муравей тогда восстанавливает его траекторию, двигаясь в противоположное руководство от d до o. Мы считаем следующие два варианта метода обновления выполненными муравьем на его поездке возвращения.
1. Метод обновления подпути: муравей обновляет оценки времени поездки в каждом из узлов ik, k = 1, 2, … , N − 1, который это посетило на передовой траектории, согласно формуле
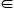(0, 1] демпфирование, или stepsize параметр, который определяет надбавку новой информации относительно предыдущей оценки, вычисляя новую оценку, и qik, ik+1, d, является временем поездки, измеренным муравьем в путешествии из узла ik к d через уходящую ссылку (ik, ik+1). Этот процесс продолжается, пока муравей не возвратился к узлу происхождения i1 = o, после чего это обновляет значение Qi1, i2, d связанный с первой ссылкой перелета передового муравья. 2. Единственный метод обновления: муравей только обновляет значение Qi1, i2, d связанный с его первой ссылкой перелета, согласно правилу
Процесс обновления Q-значения поэтому управляется муравьями, которые едут от происхождения до адресата, возможно более чем многие различные маршруты, с каждым муравьем, эффективно выполняющим измерения времени поездки на сети, и сообщающим о результатах назад узлам, в которых поддержаны специфические Q-значения.
Вообще, процесс обновления, определенный (1) или (2), был бы выполнен асинхронно для всех Q-значений.gif){kind=small}
, и для всех узлов адресата d. Асинхронизм является результатом факта, что различные муравьи испытывают различные времена поездки, в дополнение к факту, что может не обязательно быть координация всей сети создания муравья и отправки для различных пар узла адресата происхождения.
Ключевой механизм обратной связи между оценкой времени поездки и направляющей ложью в обновлении муравья и данных, направляющих вероятности. Каждый раз, когда оценка времени поездки Qijd обновлена, соответствующий муравей и данные, направляющие вероятности, также обновлены. Следующие процедуры, которые подобны предложенным в [10] и [9], это сделано согласно правилам обновления
Для значений, больше чем или равный 1, параметр β действует как “обратный температурный” параметр, который управляет степенью исследования, выполненного муравьями. Как β увеличения, отборные вероятности ссылки становятся, более резко "достиг максимума" на ссылках, для которых Q-значения являются наименьшими. Эффект - то, что увеличение значения β приводит к уменьшению к уровню исследования, выполненного муравьями.
Точно так же мы видим, что σ управляет распределением трафика данных по уходящим ссылкам, и таким образом управляет степенью, которой трафик данных распределен по многократным путям. Устанавливая β < σ, мы подражаем данным, направляющим механизм, используемый в AntNet, посредством чего у пакетов данных есть более высокая вероятность чем муравьи ссылок выбора с низкой связанной задержкой. В этой манере пакеты данных склоняются к эксплуатации ссылок с низкими связанными Q-значениями, тогда как муравьи склоняются к сетевому исследованию, на основании факта, что они, более вероятно, выберут ссылки с выше связанными Q-значениями.
В этом разделе мы развиваем аналитическую модель основанного на муравье алгоритма маршрутизации, описанного в Разделе 4. Впустите узлы быть .gif){kind=small}
маркированными я = 1, 2, … , S. Для аналитической модели мы ограничиваем свое внимание единственным узлом адресата, маркировал S. Кроме того, мы ограничиваем содержание набора к .gif){kind=small}
тем ссылкам (я, j) для который я ≠ S.
Модель изображена из себя, следует: позвольте быть .gif){kind=small}
дискретным итеративным индексом. После описания алгоритма маршрутизации в Разделе 4, позвольте 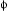ijS (β, n) быть вероятностью при итерации n маршрутизации муравья в настоящее время в узле i, чей узел адресата - S, вдоль ссылки (я, j), и позволять ψijS (β, n) быть передачей, направляющей вероятность для пакета данных. Всюду по остальной части бумаги мы опускаем приписку S в вышеупомянутых количествах, так как все количества принадлежат тому же самому узлу адресата.
Муравей, направляющий вероятности, забран в матрицу Φ (β, n) измерения (S − 1) × (S − 1), где
Вероятности маршрутизации 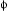(β, n) не появляются в матрице Φ (β, n), но может быть получен через отношение
Точно так же данные, направляющие вероятности, собраны в матрицу Ψ (σ, n) измерения (S − 1) × (S − 1). Маршрутизация matrices Φ (β, n) и Ψ (σ, n) уникально определяет путь, которым трафик муравья и данных направлен через сеть.
Позвольте быть .gif){kind=small}
нормой трафика муравья, вводящего сеть в узел i, который предназначен для узла S, где.gif){kind=small}
. Значения.gif){kind=small}
, я = 1, … , S − 1, забран в (S − 1) мерный вектор.gif){kind=small}
. Точно так же позвольте Сицзяну обозначать запрос трафика данных, вводящий сеть в узел i, который предназначен для узла S, и позволять s быть вектором запросов трафика данных.
Потоки узла муравья, обозначенные, даны .gif){kind=small}
в соответствии с решением системы уравнений
.gif){kind=small}
. У системы уравнений (7) есть уникальное решение, при условии, что матрица Φ (β, n) такова, что там существует путь положительной вероятности от каждого узла до .gif){kind=small}
узел адресата S [22], когда матрица, I − Φ (β, n) является обратимым и решение, может быть написана в векторной форме какПотоки узла данных, обозначенные wi (n) даны так же в соответствии с решением системы уравнений
.gif){kind=small}
узел адресата S, как выше. Получающимся муравьем и потоками канала связи даютОни собраны в вектор f (n), измерения.gif){kind=small}
.
Затем, мы развиваем модель ожидаемых задержек, понесенных муравьями и пакетами данных, поскольку они пересекают сеть. Мы начинаем, рассматривая ожидаемую задержку на каждой ссылке. Позвольте Cij быть сервисной нормой, связанной со ссылкой (я, j). Значения Cij, поскольку.gif){kind=small}
, моделируют мощности ссылки, которые конечны и строго положительны. Потоки ссылки и мощности ссылки определяют ожидаемые задержки организации очередей, связанные с пересечением сетевых ссылок. Ожидаемая задержка организации очередей, связанная с пересечением ссылки (я, j), дают
Выражение (11) - формула для ожидаемой задержки, понесенной пакетом в очереди M/M/1 [23]. Использование (11) поэтому влечет за собой предположение, что процесс прибытия пакета при ссылке (я, j) является процессом Пуассона, с нормой прибытия fij (n), и те времена обслуживания пакета по экспоненте распределены со скупым.gif){kind=small}
. Это приближение часто используется, чтобы смоделировать постоянную скупую задержку пакета очередей в пределах компьютера и систем коммуникаций [1]. В частности функция d (·, ·) увеличивается монотонно как количество потока трафика на увеличениях ссылки, и имеет тенденцию к бесконечности, поскольку поток трафика приближается к способности ссылки, и является поэтому подходящим в основной цели ввести зависимые от потока задержки ссылки в аналитическую модель. Действительно, точная форма d (·, ·) не важна с целью нашей модели, обеспечил d (·, ·) posesses вышеупомянутое (или подобный) свойства. Полная ожидаемая задержка связалась с пересечением ссылки (я, j) дают
Позвольте Qij (n), обозначают ожидаемую задержку, понесенную муравьем, который едет из узла i адресату S, через специфическую уходящую ссылку (я, j), когда муравей, направляющий матрицу, является Φ (β, n), и данные, направляющие матрицу, являются Ψ (σ, n). Мы собираем Q-значения в вектор Q (n), измерения A. Q-значения получены из муравья и данных, направляющих вероятности следующим образом.
Позвольте Jj (n), обозначают ожидаемое время, потраченное муравьем, чтобы поехать из узла j к узлу адресата S, где ожидание взято относительно текущего муравья, направляющего вероятности. Jj (n) дан в соответствии с решением системы уравнений
.gif){kind=small}
. Решение системы уравнений (13) может быть написано в векторной форме какQ-значениями тогда дают
Отметьте, что в выражении (13), суммировании по соседним узлам.gif){kind=small}
, нагружен муравьем, направляющим вероятности, Φ (β, n), а не данные, направляющие вероятности, Ψ (σ, n). Это совместимо с фактом, что это - муравей, направляющий вероятности, а не данные, направляющие вероятности, которые управляют выбором ссылки муравья.
Мы обратимся к оценке Jj (n), j = 1, … , S − 1, и Qij (n) для всех как .gif){kind=small}
Стадия 1 из аналитической модели. Стадия 2 из аналитической модели вовлекают поколение нового муравья и данных, направляющих matrices, Φ (β, n + 1) и Ψ (σ, n + 1), соответственно. После описания алгоритма маршрутизации, данного в Разделе 4, муравей, направляющий вероятности, обновлен согласно
Выражение (18), и следовательно также выражение (17), не определены, когда для данного узла i, значения Qik (n) для всех не .gif){kind=small}
конечны. Такая ситуация происходит если fij 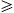Cij для всех.gif){kind=small}
. Для аналитической модели, чтобы быть четкими при этих обстоятельствах, мы произвольно устанавливаем.gif){kind=small}
, где.gif){kind=small}
.
Данные, направляющие вероятности, обновлены согласно
Как прежде, когда значения Qik (n) для всех не .gif){kind=small}
конечны, мы произвольно устанавливаем.gif){kind=small}
.
Мы можем выразить аналитическую модель, используя более компактное примечание, следующим образом. Рассмотрите (S − 1) × 2 (S − 1) матрица Π (n) = (Φ (β, n), Ψ (σ, n)), и определите отображение.gif){kind=small}
, данное
Λ отображает муравья и данные, направляющие вероятности, чтобы связать потоки. Определите отображение.gif){kind=small}
, данное
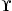муравей карт, направляющий вероятности и ссылку, задерживается к ожидаемым задержкам муравья, J (n). Определите отображение.gif){kind=small}
, данное.gif){kind=small}
(18) и (20), соответственно. Ω отображает Q-значения к муравью и данным, направляющим вероятности. Мы отмечаем, что для конечных значений β и σ, не возможно одновременно иметь и,.gif){kind=small}
.gif){kind=small}
или наоборот. Поэтому, эти возможности не должны быть рассмотрены на определении Ω. Мы можем выразить аналитическую модель как итерацию Q-значений
Ясно, что отображение хорошо .gif){kind=small}
определено при каждой итерации.gif){kind=small}
, в смысле, что matrices я − Φ (β, n) и я, Φ (σ, n) являются обратимыми, при условии, что начальные значения Q (0) строго положительны и конечны. То же самое верно для отображения.gif){kind=small}
, при условии, что начальный муравей и данные, направляющие matrices Φ (β, 0) и Φ (σ, n), каждый определяет по крайней мере один путь положительной вероятности от каждого узла до .gif){kind=small}
узла адресата S [22].
Вообще, отображения, данные в (23) и (24), не непрерывны, из-за нехватки непрерывности отображения Ω как.gif){kind=small}
. Поэтому не возможно гарантировать, что у аналитической модели есть неподвижный пункт при общих обстоятельствах. Однако, в нашем числовом опыте, мы всегда были в состоянии решить (23) и (24). Кроме того, Ω - непрерывное отображение для особого случая, который характеризован легкими запросами трафика, где fij < Cij для всех ссылок под .gif){kind=small}
всей возможной политикой маршрутизации Φ и Ψ. Этот особый случай возникает в анализе модели, представленной в Разделе 6.
Мы отмечаем, что основанный на муравье алгоритм маршрутизации, описанный в Разделе 4, неотъемлемо децентрализован и распределен. В результате обновления вероятностей маршрутизации и Q-значений происходят одновременно и асинхронно, без "глобальной" координации всей сети. Напротив, формулировка аналитической модели влечет за собой приближение к реальному основанному на муравье алгоритму маршрутизации, известному как приближение разделения шкалы времени. В частности аналитическая модель вычисляет все ожидаемые сетевые задержки точно при каждой итерации, до обновления маршрутизации при последующей итерации. Несмотря на это приближение, мы находим, что мы можем использовать аналитическую модель, чтобы получить немного важной способности проникновения в суть поведения равновесия основанного на муравье алгоритма маршрутизации.
В этом разделе мы обеспечиваем краткий обзор нашего подхода к анализу основанного на муравье алгоритма маршрутизации, описанного в Разделе 4. В частности мы комментируем возможности аналитической модели, которая была представлена выше, и природа информации, которая будет получена через ее анализ.
Мы начинаем, отмечая, что алгоритм маршрутизации, описанный в Разделе 4, должен выполнить две важных задачи. Первая задача вовлекает обновление Q-значений, используя времена поездки, испытанные муравьями. Это может быть расценено как “информация, собирающая” деятельность, где информация, которая будет собрана отношения сетевые времена поездки и задержки. Вторая задача вовлекает использование информации, содержавшейся в Q-значениях, чтобы создать данные, направляющие политику.
В Разделе 6, мы сосредотачиваемся на первой задаче, то есть, “информация, собирающая” свойства алгоритма. Чтобы сделать это, мы рассматриваем поведение агентов в отсутствии запросов трафика данных. Мы предполагаем, что загрузка, помещенная в сеть трафиком муравья, незначительна, так, чтобы муравьи испытали только закрепленную задержку передачи на каждой ссылке, которая пересечена, но никакие зависимые от потока задержки организации очередей. Получающаяся проблема оптимизации - статическая самая короткая проблема пути на сети, которая обеспечивает простой контекст, чтобы исследовать немного фундаментальных аспектов основанного на муравье алгоритма. В частности мы используем этот контекст, чтобы подсветить факт, что основанные на муравье алгоритмы маршрутизации используют ту же самую политику для исследования сети, поскольку они делают для принятия решения, которое может привести к подоптимальным решениям маршрутизации. Мы предлагаем простую модификацию механизму исследования муравья, который устраняет этот тип ошибки.
В Разделе 7, мы рассматриваем вторую задачу маршрутизации в присутствии запросов трафика данных. В этом контексте мы в состоянии изучить способность алгоритма выполнить балансирование загрузки трафика данных по многократным путям для данных пар узла адресата происхождения. Важно, там не существуйте статические самые короткие пути как пункт справочной информации, потому что ожидаемая задержка, связанная с каждым путем, зависит от потока трафика данных на пути, и следовательно зависит от текущих данных, направляющих политику.
Соответствующие пункты справочной информации для анализа равновесия алгоритма - система и пользователь оптимальные потоки трафика. Мы демонстрируем, что есть многая неэффективность, связанная с основанным на муравье алгоритмом относительно таких мер, и мы предлагаем модификации исследованию и балансированным загрузки механизмам, которые устраняют эту неэффективность.
В этом разделе мы анализируем основанный на муравье алгоритм в отсутствии запросов трафика данных, так, чтобы при всех итерациях.gif){kind=small}
, мы имели для .gif){kind=small}
всех ссылок (я, j). Кроме того, мы предполагаем, что загрузка, помещенная в сеть муравьями, незначительна, то есть.gif){kind=small}
, для всех ссылок (я, j). Задержки ссылки могут тогда быть приближены постоянными значениями.gif){kind=small}
, которые не зависят от муравья или данных, направляющих matrices, и следовательно не зависят от итеративного индекса n.
В этом сценарии сетевая проблема оптимизации уменьшает до детерминированной самой короткой проблемы пути, где цель для муравьев, чтобы идентифицировать самый короткий путь от каждого узла до узла адресата S. В частности мы можем получить сведения об эффекте, который механизм исследования, используемый муравьями, имеет на их способность выполнить эту задачу.
Как пункт справочной информации, мы рассматриваем набор “оптимальных Q-значений” [24] и [2] для детерминированной самой короткой проблемы пути, данной
.gif){kind=small}
, j = 1, … , S − 1, являются (оптимальными) самыми короткими затратами пути [25] связанный с достижением узла адресата S от узла j (с.gif){kind=small}
). Самый короткий путь от любого узла до S может тогда быть создан просто выбором в каждом узле i уходящая ссылка, которая удовлетворяет до .gif){kind=small}
узла адресата достигнут S. Этому показывают в [22], что отображение (24) является continuous3 для особого случая, где задержки ссылки являются постоянными, и поэтому имеет неподвижный пункт [26]. Кроме того, у любого такого неподвижного пункта есть .gif){kind=small}
набор передачи Q-значений, которые удовлетворяют
Действительно, результат (25) не в целом удивителен, при условии, что муравей, направляющий вероятности, обновленные согласно (17), составляет невырожденную рандомизированную политику со всеми положительными вероятностями, тогда как это известно, что оптимальная политика для самой короткой проблемы пути детерминирована [25]. В терминах поведения муравья мы видим это, в то время как некоторая фракция муравьев едет на самых коротких путях, остающемся путешествии муравьев на подоптимальных путях. Скупое время поездки, испытанное муравьями, путешествующими между данным происхождением и парой узла адресата, должно поэтому быть больше чем самое короткое время поездки между узлами.
Важно, не всегда возможно создать самый короткий путь от любого узла до адресата S просто выбором в каждом узле i уходящая ссылка, которая удовлетворяет аргумент.gif){kind=small}
. Примерам этого отказа идентифицировать самые короткие пути, основанные на Q-значениях, произведенных муравьями, показывают, используя и аналитическую модель и эксперименты моделирования, представленные в [22]. Этот тип отказа может быть понят, замечая, что самая короткая проблема пути может быть приведена как проблема решения Markov [25]; этому можно показать, что подарок рандомизации в муравье, направляющем политику эффективно, изменяет проблему решения Markov, которую муравьи пытаются решить, и при определенных обстоятельствах (см. [22]), у измененной проблемы есть оптимальная политика, которая различна к оптимальной политике для оригинальной самой короткой проблемы пути.
Это демонстрирует фундаментальную проблему, связанную с механизмом исследования, который используется основанными на муравье алгоритмами маршрутизации; то, что муравьи используют ту же самую политику для исследования, поскольку они делают для принятия решения, или заявили иначе, что нет никакого разделения между механизмом, используемым для исследования альтернативных маршрутов, и механизм имел обыкновение эксплуатировать маршруты, которые, как оценивается, оптимальны. В укреплении, изучая литературу, такой алгоритм изучения часто упоминается как то, чтобы быть "на политике" [24] и [2]. Напротив, алгоритм изучения, который обладает полным разделением между его механизмами исследования и принятия решения, упоминается как то, чтобы быть "вне политики" [24] и [2]. На языке теории [27] управления мы видим, что двойные задачи системной идентификации и управления соединены, и что есть обмен между этими задачами.
Большая часть литературы, описывающей основанные на муравье алгоритмы маршрутизации, кажется, предполагает, что этот обмен между исследованием и эксплуатацией не может быть решен, или что это сцепление не проблематично. Мы утверждаем, что дело обстоит не так, и мы представляем простую модификацию, которая может быть сделана на механизм исследования, используемый муравьями, который приводит к полному разделению исследования и эксплуатации, таким образом отдавая его алгоритм изучения вне политики.
Определенно, это достаточно, чтобы ограничить исследование муравья выбором его первой ссылки, оставляя узел происхождения, и последующие ссылки отобраны согласно правилу (17) обновления в пределе как β → ∞. Это соответствует нулевой вероятности исследования для муравья, направляющего решения во всех стадиях передового пути, за исключением первого перелета муравья, когда у всех уходящих ссылок есть положительная вероятность того, чтобы быть отобранным. Этому показывают в [22], что эта модификация к аналитической модели приводит к неподвижному пункту, который .gif){kind=small}
составляет оптимальное решение самой короткой проблемы пути, то есть, соответствующие Q-значения удовлетворяют
В Разделе 7, мы демонстрируем, что, когда запросы трафика данных помещены в сеть, свойство на политике основанных на муравье алгоритмов маршрутизации приводит к неэффективности в балансировании загрузки трафика данных, и что версия вне политики основанного на муравье алгоритма желательна в этом более типичном сценарии также.
В этом разделе мы исследуем поведение основанного на муравье алгоритма маршрутизации в присутствии запросов трафика данных. Кроме того, мы включаем в наш анализ эффекты запросов трафика муравья и потоков трафика муравья, потому что то, когда запросы трафика данных высоки, присутствие маленького количества дополнительного трафика из-за муравьев, может иметь ненезначительный эффект на задержки организации очередей.
В отличие от постоянных задержек ссылки Раздела 6, присутствие результатов потоков трафика данных в задержках ссылки, которые зависят от общей суммы трафика, который несется на ссылках. Зависимые от потока задержки ссылки возникают в результате буферизации и обработки пакетов, ждущих передачи на ссылках, у которых есть конечные мощности передачи. Это вводит сильное сцепление между трафиком, направляющим политику, и задержками, которые испытаны пакетами на каждой ссылке, и взаимодействие потока трафика с сетью - поэтому важное рассмотрение.
Кроме того, взаимодействие различных потоков трафика друг с другом - также важное рассмотрение, при условии, что многократные потоки трафика могут эффективно "конкурировать" за конечные общедоступные ресурсы, состоявшие буферами пакета и способностью передачи. Это добавляет сложность к оценке данной маршрутизации политики; сценарий оптимизации больше не простая (статическая) самая короткая проблема пути, как обсуждается в Разделе 6. Например, специфическая политика маршрутизации может быть выгодной для одного потока трафика, но вредной для другого, согласно некоторому критерию качества работы, такой как задержка в модуль переданного трафика. Это приводит к понятию "пользователей", и пользовательскому равновесию или пользовательским оптимумам. Альтернативно, средний критерий качества работы всей системы может использоваться, чтобы оценить данную маршрутизацию политики, таким образом приводя к понятию системного оптимума.
Основанные на муравье алгоритмы маршрутизации, такие как AntNet не были проектированы ни с каким определенным понятием равновесия в памяти, а скорее как тип "лучшего усилия", направляющий алгоритмы [9] и [1]. Анализ основанных на муравье алгоритмов был выполнен почти исключительно через эксперименты моделирования, которые сосредотачиваются на переходных мерах работы и восстановления в ответ на сетевые изменения. AntNet, как сообщали, выступал очень хорошо против таких мер [9].
Хотя адаптивные переходные свойства основанных на муравье алгоритмов маршрутизации чрезвычайно важны, авторы полагают, что поведение равновесия этих алгоритмов - также важное рассмотрение. В частности в дополнение к обладанию способностью реагировать быстро на сетевые изменения, основанный на муравье алгоритм маршрутизации должен также сходиться к "эффективному" равновесию, направляющему политику во время (возможно короткий) периоды, в которые сетевые условия не изменяются значительно.
В этом разделе мы демонстрируем, что текущий дизайн основанных на муравье алгоритмов маршрутизации приводит к определенной неэффективности относительно равновесия основанные на задержке меры, и мы предлагаем усовершенствования их дизайну, которые улучшают их работу, не ставя под угрозу их желательные переходные адаптивные свойства. Мы начинаем, давая краткий обзор понятий оптимизации трафика равновесия.
Анализ равновесия трафика на сетях произошел с работой Wardrop [17], который развивал средство для анализа и характеристики потоков трафика транспортного средства на дорожных сетях. Первый Принцип Wardrop’s может быть заявлен эквивалентно следующими тремя способами:
или“Время прохождения на всех используемых путях между происхождением и пунктом адресата равно, и меньше чем те, которые были бы испытаны единственным транспортным средством на любом неиспользованном пути”
или“Никакой путешественник не может улучшить свое время прохождения, односторонне изменяя маршруты”
“Каждый путешественник следует за минимальным путем времени прохождения”.
Если мы заменяем "путешественника" и "транспортное средство" с "пакетом" на вышеупомянутых определениях, мы получаем соответствующее определение для равновесия Wardrop в основанной на пакете системе коммуникаций. В частности трафик данных, направляющий политику Ψ, соответствует равновесию Wardrop, если никакой пакет не может односторонне уменьшить свое время поездки от его происхождения до адресата следующим за политикой, которая различна к Ψ.
Равновесию Wardrop позже показали, чтобы быть особым случаем равновесия Nash [28], таким образом основывая подключение между исследованием равновесия трафика на теорией [15] игры и сетях. Это подключение с тех пор использовалось экстенсивно в анализе и характеристике сети, направляющей алгоритмы и их свойства равновесия (см. например [29], [30] и [31]).
Nash и равновесие Wardrop - примеры пользовательского равновесия [28], которые возникают в сетевом контексте, когда многие пользователи конкурируют за ряд общедоступных конечных ресурсов. В контексте системы коммуникаций разделенные ресурсы соответствуют конечно-полным ссылкам. Пользователь, как могут полагать, является потоком трафика, или запросом трафика, и каждый пользователь поэтому связан с данной парой узла адресата происхождения.
Равновесие Wardrop возникает как примеры равновесия Nash в пределе, поскольку общее количество пользователей становится бесконечно большим, но где каждый индивидуальный пользователь оказывает незначительное влияние на задержки, испытанные другими пользователями [32]. В контексте основанной на пакете системы коммуникаций подключения меньше, которую рассматривают здесь, физическая интерпретация этого предела - тот, в котором пользователи соответствуют индивидуальным пакетам.
Вообще, пользовательское равновесие характеризовано "эгоистичным" поведением пользователей. Таким образом, каждый пользователь принимает решения маршрутизации, чтобы уменьшить ее собственную понесенную стоимость (в модуль направленного трафика), не учитывая эффект, который его собственные решения могут иметь на затраты, понесенные другими пользователями. Поэтому пользовательское равновесие иногда упоминается как конкурентоспособное, или несовместное равновесие [30] и [31].
Напротив, системный оптимум достигнут, когда полная средняя задержка пакета свернута по набору всех возможных решений маршрутизации, и характеризована условием, что у всех маршрутов между происхождением и узлом адресата, которые фактически используются, есть равная крайняя задержка, которая является меньше чем крайняя задержка, связанная со всеми альтернативными неиспользованными маршрутами [1].4
Факт, что основанные на муравье алгоритмы маршрутизации обновляют Q-значения и маршрутизацию вероятностей, основанных на измерениях времени поездки муравья, а не крайних измерениях задержки, предполагает, что маловероятно, что основанные на муравье алгоритмы маршрутизации, вообще, достигли бы политики маршрутизации, которая соответствует системному оптимуму. Действительно, алгоритмы, такие как AntNet не предъявляют права на цель системной оптимальной маршрутизации [9], и предложены их авторами как альтернатива самому короткому пути, направляющему алгоритмы, которые широко используются в современных системах коммуникаций [1] и [14].
Кроме того, мы не ожидаем, что у основанных на муравье алгоритмов маршрутизации должна быть способность систематически достигнуть общего пользователя (Nash) равновесие из-за "не имеющего гражданства" [1] природа маршрутизации трафика данных, посредством чего узлы дифференцируют поступающие пакеты данных соответственно только к их узлу адресата, а не согласно их узлу происхождения или предшествующей "истории". Определенно, так как все пакеты, достигающие узла, у которых есть тот же самый адресат, направлены согласно единому набору маршрутизации вероятностей, тогда никакой узел не может действовать исключительно от имени никакого пользователя или подмножества пользователей.
Действительно, алгоритмы, которые проектированы, чтобы достигнуть равновесия Nash, позволяют каждому пользователю управлять потоком их собственного трафика в каждом узле, который доступен для пользователя. Это обычно достигается, распределяя каждому пользователю конечный набор путей, и разрешая пользователю принять решения маршрутизации в ответ на решения, принятые другими пользователями [30] и [31]. Ясно, этот тип управления находится вне возможностей основанных на муравье алгоритмов маршрутизации (без главных модификаций) и других не имеющих гражданства алгоритмов маршрутизации.
Несмотря на то, что системная оптимальная и маршрутизация равновесия Nash (вообще) вне возможностей того, что достижимо не имеющим гражданства алгоритмом маршрутизации, это существенно, что равновесие Wardrop весьма совместимо с не имеющей гражданства маршрутизацией. Определенно, в Разделе 8 мы развиваем версию вне политики основанного на муравье алгоритма маршрутизации, который в состоянии добиться равновесие Wardrop.
В этом разделе мы используем аналитическую модель, чтобы исследовать некоторые из свойств основанного на муравье алгоритма маршрутизации в присутствии запросов трафика данных. Для каждого случая, который мы исследуем, мы сравниваем свои результаты с полученными из экспериментов моделирования. Мы начинаем, обеспечивая краткое описание модели моделирования, и методы имели обыкновение сравнивать вывод моделирования с аналитической моделью.
Модель моделирования состоит из тренажера дискретного случая уровня пакета, который был проектирован, чтобы отразить особенности основанного на муравье алгоритма и сети, которые зафиксированы в аналитической модели. Главные особенности модели моделирования следующие.
Есть единственный узел адресата, маркировал S, и пакеты данных созданы как поток Пуассона между парами узла адресата происхождения (я, S), поскольку я = 1, … , S − 1, в неподвижных нормах, данных Сицзяном 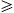0. Пакеты муравья созданы как поток Пуассона между парами узла адресата происхождения (я, S), поскольку я = 1, … , S − 1, в неподвижных нормах, данных.gif){kind=small}
, где число .gif){kind=small}
соседних узлов узла i, и k > 0, являюсь параметром, который управляет нормой эмиссии муравьев относительно эмиссии пакетов данных. Для моделирований, представленных в этом разделе, мы устанавливаем k = 0.01. Причина для этого состоит в том, чтобы сделать загрузку трафика муравья маленькой по сравнению с загрузкой трафика данных, как предназначено в предыдущих исследованиях моделирования основанных на муравье алгоритмов маршрутизации такой как [9].
Муравьи и пакеты данных ведут себя как описано в Разделе 4. По причинам, которые будут обсуждены в следующем разделе, муравьи используют единственный метод обновления, и нет никакого механизма, чтобы препятствовать тому, чтобы муравьи или пакеты данных выполнили петли. Все пакеты (включая муравьев) достижение ссылки (я, j), помещены в единственный сервер в порядке поступления очередь [23], где сервисные времена по экспоненте распределены со скупым.gif){kind=small}
. Как только пакет оставляет очередь, он испытывает неподвижную задержку передачи ссылки rij. Полная задержка, испытанная пакетом на ссылке, дана суммой случайного количества времени, потраченного в очереди (включая сервисное время), и детерминированная задержка передачи ссылки.
Обновления муравья и данных, направляющих вероятности в данном узле я, вызваны всякий раз, когда обновление к Q-значению, Qij, для происходит.gif){kind=small}
. Муравей и данные, направляющие обновления, выполнены согласно Рис. (3) и (4).
Модель моделирования таким образом состоит из сети очередей M/M/1, с источниками трафика Пуассона, происходящими в узлах. Модель моделирования была утверждена, сравнивая скупые оценки задержки пакета в сети с их известными математическими ожиданиями под неподвижной политикой маршрутизации. Чтобы утвердить механизмы для того, чтобы обновить политику маршрутизации, модель моделирования была сравнена с известными испытательными случаями.
Данные от модели моделирования собраны следующим образом. Пробуя Qij.gif){kind=small}
, в регулярных временных интервалах моделирования, мы создаем временной ряд для каждого Q-значения. Значение равновесия Qij оценено, беря среднее число соответствующего временного ряда, как только система достигла равновесия. Для каждого примера, описанного в этой газете, мы производим 10 ответов, чтобы получить оценки равновесия.gif){kind=small}
, так же как связанные 95%-ые доверительные интервалы. Они могут использоваться, чтобы сравнить поведение равновесия модели моделирования с неподвижным пунктом аналитической модели.
Мы рассматриваем сначала стандартный случай операции основанного на муравье алгоритма маршрутизации, где параметры β и σ конечны и больше чем единство. Выберите, что β параметризует степень исследования, которое выполнено муравьями и σ, управляет степенью, до которой трафик данных направлен по многократным путям. Устанавливая σ < ∞ учитывает некоторую фракцию трафика данных, который будет направлен на ссылках, у которых нет минимальных связанных Q-значений, таким образом эффективно "распространяя" запрос трафика по альтернативным путям, и идеально, приводя к определенной степени загрузки балансирующий из трафика данных.
Как правило, можно было бы выбрать β < σ, так, чтобы по сравнению с муравьем, направляющим вероятности, данные, направляющие вероятности, были более резко "достигнуты максимума" при уходящих ссылках с минимальными связанными Q-значениями. Рассуждение позади такой схемы - то, что у муравьев должна, собственно говоря, быть большая склонность к исследованию, тогда как у пакетов данных должна быть большая склонность к эксплуатации путей с ниже предполагаемой задержкой. Действительно, это - одна из стратегий, используемых алгоритмом AntNet [9].
Считайте сеть с четырьмя узлами показанной в рис. 1. Позвольте Cij = 10 и rij = 0.1, для всех.gif){kind=small}
. Узел адресата - S = 4. Мы начинаем, расследуя пример, где загрузка трафика легка, с векторным s запроса трафика данных = (5, 5, 0, 0). Нормой трафика муравья, вводящего сеть, дают.gif){kind=small}
, так, чтобы.gif){kind=small}
, с k = 0.01.
Рис. 1. Четыре сети узла. Адресат - узел 4.
Позвольте β = 2, σ = 4, с начальным условием Qij (0) = 1 для всех.gif){kind=small}
. Для аналитической модели мы осуществляем следующую заглушенную версию итерации (23):
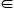(0,1] параметр демпфирования. Значение параметра демпфирования не имеет никакого эффекта на неподвижные пункты, полученные из аналитической модели, и служит просто, чтобы произвести "гладкие" траектории с переходным поведением, которое близко напоминает поведение реальной системы. Траекториям Q-значений, полученных из числовой итерации аналитической модели, показывают в рис. 2. Есть восемь индивидуальных траекторий, соответствуя Q-значениям для.gif){kind=small}
, исключая те для который я = S = 4. Передача моделировала траектории, произведенные при использовании единственного метода обновления (см. Раздел 4), показаны в рис. 3. Каждая траектория получена, беря “pointwise” среднее число более чем 10 независимых моделирований.
Рис. 2. Траектории Q-значения получены из итерации аналитической модели (27).
(23 КБ)
Рис. 3. Траектории Q-значения, полученные через моделирование основанного на муравье алгоритма маршрутизации, используя единственный метод обновления.
Сравнивая рис. 2 и рис. 3, мы видим, что аналитическая модель фиксирует несколько из качественных особенностей моделируемых траекторий. Несмотря на приближение разделения шкалы времени, мы замечаем, что траектория, произведенная нашей моделью, в состоянии фиксировать переходное поведение модели моделирования для этого примера.
Из самого большого интереса Q-значения равновесия, которые получены в итоге в Таблице 2. Первый столбец Таблицы 2 содержит индексы.gif){kind=small}
. Второй столбец содержит входы вектора.gif){kind=small}
, который является полученным использованием неподвижного пункта аналитической модели. Третий столбец содержит 95%-ые доверительные интервалы для значений равновесия.gif){kind=small}
, получил использование модели моделирования с единственным методом обновления. Количества вычислены .gif){kind=small}
как описано в Разделе 7.2.1. Это замечено в Таблице 2, что все входы лжи .gif){kind=small}
в пределах соответствующих 95%-ых доверительных интервалов для.gif){kind=small}
.
Легкий пример загрузки трафика с запросом трафика данных направляет s = (5, 5, 0, 0)
Интересно отметить, что во многих экспериментах, мы нашли там, чтобы быть различиями между доверительными интервалами для Q-значений равновесия, полученных из экспериментов моделирования, используя подпуть и единственные методы обновления, соответственно [22]. Это различие может быть приписано статистическому уклону, связанному с методом обновления подпути, который является результатом факта, что некоторые муравьи выполняют петли, и таким образом повторно посещают один или более узлов на их передовом пути. Времена поездки, зарегистрированные от каждого повторно посещаемого узла до адресата, поэтому коррелированы, так как измерение времени поездки, связанное с первым посещением узла, обязательно больше чем измерение времени поездки, связанное с последующим посещением, и т.д для каждого перепосещения. Эта корреляция вводит статистический уклон относительно Q-значений.gif){kind=small}
, произведенный аналитической моделью, которые являются математическими ожиданиями в течение времен поездки, связанных с достигающим узлом S через каждую из ссылок в.gif){kind=small}
. Природа этого уклона обсуждается более подробно с примерами в [22], и следует за анализом коррелированых траекторий в методах Монте Карло для изучения укрепления, как обсуждается в [1]. В этой газете мы используем единственный метод обновления в модели моделирования.
Мы отмечаем, что основанные на муравье алгоритмы маршрутизации типично используют метод обновления подпути, поскольку это делает более эффективное использование информации собранным каждым муравьем и приводит к более быстрой норме конвергенции. Если метод обновления подпути используется, то основанные на муравье алгоритмы маршрутизации типично также включают меры, чтобы противодействовать типу уклона последовательного выбора поездки, описанного выше, самое общее существо механизм предотвращения перекручивания (см., например, [9]). Мы хотели не моделировать механизм предотвращения перекручивания в нашей аналитической модели, поскольку это делало бы аналитическую модель тяжелой, и не будет обеспечивать дополнительного понимания поведения равновесия системы, которая является первичной целью этой бумаги.
Четвертые и пятые столбцы Таблицы 2 показывают значениям муравья и данных, направляющих вероятности в неподвижном пункте, обозначенном и,.gif){kind=small}
.gif){kind=small}
соответственно. Как ожидается, учитывая выборы β = 2 < σ = 4, данные, направляющие вероятности, более резко "достигнуты максимума" на ссылках с наименьшими связанными Q-значениями. Рассмотрите, например, Q-значения.gif){kind=small}
. У обоих муравьев и данных есть большая вероятность выбора, ссылка (1, 3), то есть, и,.gif){kind=small}
.gif){kind=small}
но эта вероятность больше для данных чем муравьи, то есть.gif){kind=small}
.
Шестой столбец Таблицы 2 содержит входы ожидаемого вектора потока трафика данных, fdata, произведенный матрицей маршрутизации.gif){kind=small}
. Мы можем сравниться, fdata с потоком направляет fsys и fwar, которые содержат потоки ссылки, связанные с системным оптимумом и равновесием Wardrop для этой проблемы. Им показывают в последних двух столбцах Таблицы 2, соответственно.
Осмотром мы видим, что потоки равновесия, достигнутые аналитической моделью, не соответствуют или системному оптимуму или равновесию Wardrop. То же самое может быть надежно выведено для потоков, произведенных моделью моделирования, с тех пор от Таблицы 2, мы видим, что.gif){kind=small}
, и установившийся поток трафика, вводящего каждую ссылку, настоятельно соединен к Q-значениям через вероятности маршрутизации (и подчинено только стохастическим колебаниям, следующим из рандомизированной природы маршрутизации пакета). В вычислительном отношении, мы можем сравнить fdata с векторами потока fsys и fwar, относительно основанных на системе и основанных на пользователе критериев качества работы, следующим образом.
Системный критерий качества работы, который мы рассматриваем для данного вектора потока, f, является полной средней задержкой пакета, данной
Критерии качества работы для легкого трафика загружают пример
fsys fwar fdata Utotal (f) 4.41 4.42 4.68 0.55 0.54 0.56 0.33 0.34 0.38
Пакет (пользователь) критерии качества работы, связанные с данным вектором потока, является определенным для каждой индивидуальной o–d пары. Для данной o–d пары (я, 4), критерий качества работы пакета, связанный с данной маршрутизацией матрицы Ψ и векторный fdata потока, ожидаемая задержка, понесенная единственным пакетом данных, едущим от меня до 4, данный ith входом вектора.
.gif){kind=small}
.gif){kind=small}
для каждого из потоков fsys, fwar, и fdata. Мы видим этоПодобные результаты наблюдаются, когда загрузка трафика на сети выше. Полагайте, что тот же самый пример, но с запросом трафика данных направляют s = (10, 2, 0, 0). Результаты получены в итоге в Таблице 4, где замечено что все входы лжи .gif){kind=small}
в пределах 95%-ых доверительных интервалов для.gif){kind=small}
.
Более тяжелый пример загрузки трафика с запросом трафика данных направляет s = (10, 2, 0, 0)
Как прежде, мы можем сравнить fdata с векторами потока fsys и fwar, относительно основанных на системе и основанных на пользователе критериев качества работы. Этому сравнению показывают в Таблице 5.
Критерии качества работы для более тяжелого трафика загружают пример
fsys fwar fdata Utotal (f) 7.31 7.41 7.71 0.66 0.66 0.68 0.37 0.38 0.40
В резюме вычисления, которым показывают в Таблице 3 и Таблице 5 для легких и тяжелых примеров загрузки трафика, соответственно, демонстрируют, что потоки трафика данных, произведенные аналитической моделью и основанным на муравье алгоритмом маршрутизации, подоптимальны и относительно системы и относительно пользовательских критериев качества работы.
Вообще, эта неэффективность возникает, потому что основанный на муравье алгоритм маршрутизации обладает только ограниченной способностью балансировать загрузку трафика в пути, который является определенным для условий, с которыми сталкиваются на уходящих ссылках в каждом сетевом узле. Например, мы видели в примере, полученном в итоге в Таблице 2, что даже при том, что трафик назначен на уходящие ссылки в манере, которая отражает относительные величины связанных Q-значений, использование конечного значения σ означает, что невозможно установить поток трафика в ноль на определенных ссылках, или наоборот, послать весь трафик исключительно на единственной уходящей ссылке, если это, случается, более эффективно от пользовательской точки зрения или системы.
Конечно, "наивное", хотя очень обычный [14] подход к устранению вышеупомянутой неэффективности (включая петли), должно было бы позволить пакетам данных исключительно следовать за ссылками, которые, как оценивают муравьи, лежат на путях наименее стоимости. Это составило бы форму самого короткого пути, направляющего [1], у которого, поскольку мы обсудим в Разделе 7.2.3, есть его собственный набор связанных проблем, самыми известными из которых является колебательной политикой маршрутизации, и неспособностью выполнить эффективную балансирующую загрузку, когда запросы трафика высоки.
Это поднимает вопрос того, как основанный на муравье алгоритм маршрутизации мог обеспечить эффективное балансирование загрузки, также эксплуатируя пути с низкой связанной задержкой, чтобы устранить неэффективность в данных, направляющих политику. Мы обращаемся к этой проблеме в Разделе 8.
Увеличение значения балансированного загрузки параметра σ уменьшает количество трафика данных, который едет на очень высоких маршрутах задержки. Окончательный результат этого происходит, если мы позволяем σ → ∞. В этом пределе мы видим от (4), тот трафик данных был бы направлен исключительно на ссылках с минимальными связанными Q-значениями. Мы отмечаем, что такие данные, направляющие механизм, соответствуют самому короткому пути, направляющему [1], но из-за уравнения (19), учитывает равное совместное использование, если у многократных путей есть та же самая предполагаемая задержка.
Самая короткая маршрутизация пути трафика данных - выполнимая опция, когда загрузка трафика на сети легка. Однако, под тяжелым трафиком загружают условия, это известно, что адаптивная самая короткая маршрутизация пути может привести к определенным ссылкам, становящимся перегруженной, приводя к нежелательным колебаниям в политике маршрутизации [1] и [37]. Действительно, мы наблюдали подобный instabilities в наших аналитических моделях и моделях моделирования, когда σ установлен в большое значение [22].
В этом отношении, эвристические данные, направляющие механизм, используемый основанным на муравье алгоритмом маршрутизации, являются более здравыми чем самая короткая маршрутизация данных пути, когда загрузка трафика, помещенная в сеть, высока. Мы отмечаем, что в экспериментах моделирования, выполненных в [9], AntNet, как находили, выступал лучше чем конкурирующие алгоритмы, точно из-за врожденной загрузки, балансирующей способность, которая предоставлена при помощи рандомизированных данных, направляющих политику. Алгоритмы маршрутизации, что AntNet был по сравнению с в [9], включали OSPF [14], Распределенный Форд глашатая [1], Q-маршрутизация [3], и PQ-маршрутизация [4]. Все они использовали самый короткий путь (в противоположность многопутевому) направляющий для трафика данных, и поэтому испытывали недостаток в способности эффективно выполнить балансирующую загрузку. Это было одной из первичных причин, по которым вышеупомянутые алгоритмы, как находили, сравнились плохо с AntNet во многих ситуациях.
Анализ, представленный в Разделах Разделов 6 и 7, предполагает, что эффективность основанных на муравье алгоритмов маршрутизации может быть улучшена, делая многие модификации к их основной операции, которую мы описываем в этом разделе. Определенно, мы наблюдали в Разделе 6, что основанные на муравье алгоритмы маршрутизации на политике изучают алгоритмы & #x5b; 24] и [2], что означает, что муравьи используют ту же самую политику для исследования, поскольку они используют для "принятия решения". Это может привести к отказу правильно идентифицировать самые короткие пути в контексте, где затраты ссылки установлены.
В присутствии запросов трафика данных задержки ссылки зависят от количества трафика данных, который несется на них, и также, там не существуйте статические самые короткие пути на сети. Однако, аналогичные проблемы возникают, когда задержки ссылки зависимы от потока. Определенно, природа на политике основанных на муравье алгоритмов маршрутизации влечет за собой свойство, что муравьи используют ту же самую политику, Φ, выполнить задачу исследования новых маршрутов так же как оценить времена поездки, испытанные пакетами данных. Это нежелательно по следующим причинам:
1. Так как муравьи и пакеты данных направлены согласно различной политике (Φ и Ψ, соответственно), распределение времен поездки, испытанных муравьями, различно к этому в течение времен поездки, испытанных пакетами данных, и соответствующие средства различны вообще. В результате Q-значения, которые основаны на измерениях времени поездки муравья, фактически "встревожены" относительно задержек, испытанных пакетами данных. Следовательно, данные, направляющие решения, основаны на этих встревоженных оценках, а не оценках фактических задержек трафика данных.
2. Есть врожденное сцепление между задачами маршрутизации муравья, сетевого исследования, и маршрутизации данных (который включает задачу балансирования загрузки), и в результате волнение, описанное в (1) аффекты все эти задачи одновременно.
3. Волнение и сцепление, описанное выше, приводят к неэффективной маршрутизации данных относительно пользователя и основанных на системе критериев качества работы равновесия, как демонстрируется в Разделе 7.
Хотя основанные на муравье алгоритмы маршрутизации достигают определенной степени дифференцирования между задачами маршрутизации данных и сетевого исследования (например, устанавливая β < σ < ∞), мы видим, что это сцепление не может быть устранено, не делая немного фундаментальных изменений к пути, которым выполнены эти задачи.
Вышеупомянутые рассмотрения мотивируют наше предложение версии вне политики основанного на муравье алгоритма маршрутизации, который проектирован, чтобы устранить источники неэффективности, которую мы идентифицировали. Модификации, которые мы предлагаем, достигают полного разделения между задачами сетевого исследования и оценки задержки, поддерживая привлекательные свойства основанных на муравье алгоритмов маршрутизации.
Версия вне политики алгоритма может быть достигнута следующим образом. Как описано в Разделе 6, исследование муравья может быть поддержано, разрешая муравьям выполнить исследование только на их первом перелете. Для последующих решений муравьи следуют за текущими данными, направляющими политику, Ψ. Результат состоит в том, что времена поездки муравья, и следовательно Q-значения, отражают задержки, понесенные пакетами данных. В частности значение Qij составляет оценку задержки, которая была бы понесена пакетом данных в узле i, если это должно было выбрать уходящую ссылку (я, j), под текущими данными, направляющими политику, Ψ. Это контрастирует с оригинальной версией на политике базируемого алгоритма муравья, в котором муравьи и данные используют различную политику маршрутизации, так, чтобы "представление" сетевых задержек, состоявших Q-значениями, точно не отразило задержки трафика данных.
Кроме того, ограничивая исследование муравья первым перелетом, мы в состоянии расцепить механизм исследования от данных, направляющих политику Ψ. Версия вне политики алгоритма поэтому только требует единственной политики маршрутизации Ψ для обоих муравьев и пакетов данных, так же как первого механизма исследования перелета для муравьев. Действительно, любой механизм исследования, который назначает вероятность отличную от нуля на каждую ссылку, выбирая первый перелет муравья, в принципе, достаточен [24] и [2].
Кроме того, мы предлагаем альтернативный механизм обновления для данных, направляющих матрицу Ψ, который не ограничивает данные, направляющие вероятности далеко от значений 0 и 1. Механизм, который мы представляем, приспособлен от одного используемого в [36], где мы заменили крайние оценки задержки в [36], с Q-значениями, используемыми основанным на муравье алгоритмом маршрутизации.
Вместо того, чтобы обновить данные, направляющие матрицу согласно правилу (4), обновления выполнены следующим образом. Предположите Q-значение в узле, я обновлен муравьем. В этом данном пункте вовремя, позвольте быть .gif){kind=small}
подмножеством ссылок для .gif){kind=small}
который
Данные, направляющие вероятности, тогда обновлены согласно правилу
Мы видим от (31), что эта процедура обновления увеличивает количество трафика данных, который направлен на ссылках с минимальными связанными Q-значениями, и декрементах количество трафика данных, который направлен на всех других ссылках. От (29), мы видим, что величинами приращений и декрементов управляет количество, которым Q-значения отклоняются от минимальных Q-значений.gif){kind=small}
, так же как величины параметра отклонения потока λ.
Присутствие срока в .gif){kind=small}
знаменателе на правой стороне (29), подачи, чтобы масштабировать размер приращений и декрементов так, чтобы они остались совместимыми с порядком величины текущих Q-значений. Процедура (31) обновления сохраняет нормализацию вероятностей маршрутизации, и минута {·, ·}, операция в (29) предотвращает вероятности маршрутизации от когда-либо становления отрицательным.
Нужно отметить, что данные, направляющие процедуру обновления, данную Рис. выражений (28), (29), (30) и (31), не предотвращают данных данных, направляющих вероятность, ψij, от становления равным нолю (или от остающегося равный нолю, раз так инициализированному). В этом случае, достаточное исследование альтернативных маршрутов поддержано муравьем, сначала прыгают через механизм исследования.
Аналитическая модель, представленная в Разделе 5, может быть прямо приспособлена, чтобы представить версию вне политики основанного на муравье алгоритма маршрутизации. Это описано в Приложении A, где мы показываем этому, аналитическая модель для алгоритма вне политики может быть выражена как итерация данных, направляющих вероятности
Отображение (32) повторено для четырех сетей сети узла, которым показывают в рис. 1, с Cij = 10 и rij = 0.1, для всех.gif){kind=small}
, и запрос трафика данных направляет s = (2, 10, 5, 0). Запросами трафика муравья снова дают.gif){kind=small}
, с и .gif){kind=small}
k = 0.01. stepsize и параметры отклонения потока установлены в γ = 0.01 и λ = 0.001, соответственно. Аналитические результаты и результаты моделирования получены в итоге в Таблице 6, где замечено, что входы находятся в пределах .gif){kind=small}
95%-ых доверительных интервалов для.gif){kind=small}
. Мы отмечаем, что для этого и следующих экспериментов, мы приспособили модель моделирования, описанную в Разделе 7.2.1, чтобы осуществить модификации вне политики.
Результаты для алгоритма вне политики
Выберите определение равновесия Wardrop, данного в Разделе 7.1. Это предусматривает, что матрица маршрутизации Ψ соответствует равновесию Wardrop, если для всех пар узла адресата происхождения у путей, которые несут строго положительный поток данных, есть минимальная задержка под Ψ, и все неиспользованные пути (которые несут нулевой поток данных), имеют задержку, которая больше чем или равна минимальной задержке под Ψ.
От Таблицы 6, мы видим, что потоки трафика данных в неподвижном пункте, fdata, являются тем же самым как потоками равновесия Wardrop fwar. Мы можем проверить, что fdata соответствует равновесию Wardrop, рассматривая задержки, связанные с путями в сети.
Чтобы вычислить путь задерживается для этого примера, мы используем задержки ссылки, Rdata, которым показывают в последнем столбце Таблицы 6. Рассмотрите, например, o–d пару (1, 4). Один возможный путь между узлом 1 и узлом 4 {1, 3, 4}. Полной задержкой на этом пути дают.gif){kind=small}
. Этот путь несет положительный поток данных, потому что и .gif){kind=small}
оба .gif){kind=small}
положительны. Повторяя эту процедуру, полная задержка и состояние потока всех путей в сети могут быть определены, как показано в Таблице 7 (исключая те, которые содержат петли, так как есть бесконечное число таких путей, и мы можем видеть от Таблицы 7, что все такие пути несут нулевой поток).
Путь задерживается для примера, полученного в итоге в Таблице 6
пара o–d Путь Полная задержка Поток (1, 4) {1, 2, 4} 1.11 Нет {1, 3, 4} 0.92 Да {1, 2, 3, 4} 1.11 Нет {1, 3, 2, 4} 1.33 Нет (2, 4) {2, 4} 0.91 Да {2, 3, 4} 0.91 Да {2, 1, 3, 4} 1.12 Нет (3, 4) {3, 4} 0.70 Да {3, 2, 4} 1.11 Нет {3, 1, 2, 4} 1.31 Нет
У путей, которые несут положительный поток данных, обозначенный "да" в последнем столбце Таблицы 7, есть меньшие задержки чем все другие (неиспользованные) пути. Поэтому, матрица маршрутизации производит .gif){kind=small}
равновесие Wardrop.
Мы заключаем этот раздел, рассматривая пример большей сети, которой показывают в рис. 4. Сеть имеет 24 узла и 72 ссылки, и основана на сети GEANT, панъевропейской сети передачи данных для исследования и образования. Мощности ссылки обозначены в рис. 4, и задержки передачи ссылки определены географическим расстоянием. Для эксперимента мы позволяем адресату быть узлом S = 24, и мы позволяем вектору запроса трафика данных быть
Рис. 4. Двадцать четыре сети узла. Адресат - узел 24.
Запросами трафика муравья дают.gif){kind=small}
, я = 1, … S − 1, с и .gif){kind=small}
k = 0.01. Что касается меньших сетевых примеров, мы нашли, что все входы неподвижного вектора пункта находятся в пределах .gif){kind=small}
соответствующих 95%-ых доверительных интервалов для.gif){kind=small}
, выбор которого показаны в Таблице 8 (мы не показываем Q-значениям, связанным со всеми ссылками из-за космических ограничений). Мы также замечаем, что потоки ссылки, произведенные аналитической моделью алгоритма вне политики, совпадают с потоками равновесия Wardrop.
Отобранные результаты для алгоритма вне политики: 24 сети узла
Оказывается, что свойство равновесия Wardrop, наблюдаемое в вышеупомянутых примерах, является фактически общим свойством любого неподвижного пункта итерации (32), как заявлено в Теореме 1 ниже.
Позвольте быть .gif){kind=small}
набором всей маршрутизации matrices Ψ [0,1] (s-1) 2, для которого соответствующие полные потоки ссылки удовлетворяют fij < Cij для всех.gif){kind=small}
.
Теорема 1
Если матрица маршрутизации - .gif){kind=small}
неподвижный пункт аналитической модели для алгоритма вне политики, то .gif){kind=small}
потоки сети урожаев, которые соответствуют равновесию Wardrop.
Доказательство
От Рис. (29), (30) и (31), это прямо, чтобы показать этому, если матрица маршрутизации Ψ является неподвижным пунктом аналитической модели вне политики, то для любой ссылки (я, j) с ψij > 0 (соответствие ссылке на используемом пути), мы имеем.gif){kind=small}
, и для любой ссылки с ψij = 0 (неиспользованная ссылка), мы имеем.gif){kind=small}
. Это условие соответствует качественному определению равновесия Wardrop, данного в Разделе 7.1. Формальное доказательство от первых принципов, используя стандартную теорию нелинейной оптимизации, дано в [22]. 
Мы отмечаем, что для любого приведенного примера проблемы, членство набора определено .gif){kind=small}
взаимодействием запросов трафика, сетевой топологии и мощностей ссылки. В частности если пусто,.gif){kind=small}
то невозможно нести данные запросы трафика, не нарушая по крайней мере одно полное ограничение. Таким образом, по существу .gif){kind=small}
содержит всю "разумную" маршрутизацию matrices, и ее гипотеза в Теореме 1 не является ограничительной, кроме в случае очень плохо проставленной размеры сети.
Наконец, мы отмечаем, что равновесие Wardrop, направляющее политику, по определению, без петель. Поэтому, версия вне политики основанного на муравье алгоритма маршрутизации производит равновесие, направляющее matrices Ψ, которые без петель для обоих муравьев и пакетов данных, без потребности в отдельном механизме предотвращения перекручивания.
Исследование, представленное в этой газете, поднимает многие важные проблемы, к которому нужно обратиться в будущем развитии основанных на муравье и связал алгоритмы маршрутизации. В частности мы идентифицировали свойство на политике, которое является врожденным от текущего дизайна основанных на муравье алгоритмов маршрутизации. Это свойство - результат факта, что муравей и данные, направляющие политику, неотъемлемо соединены на механизм исследования муравья, и результаты во многих проблемах и неэффективности, описанной в Разделах Разделов 6 и 7.
Как первый шаг к адресации к этим проблемам, мы развили версию вне политики основанного на муравье алгоритма маршрутизации, и мы продемонстрировали, что это в состоянии достигнуть политики маршрутизации, которая соответствует форме основанной на пользователе оптимизации, известной как равновесие Wardrop. Модификации, что мы предлагаем результат в разъединении задач сетевого исследования, оценки задержки и балансирующей загрузки.
Хотя модели моделирования составляют очень ценный исследовательский инструмент в области основанной на муравье маршрутизации, мы продемонстрировали, что полезная способность проникновения в суть может быть получена через развитие и исследование аналитической модели и ее теоретических свойств. Работа, представленная в этой газете, устанавливает аналитическую структуру, в пределах которой могут быть смоделированы основанные на муравье алгоритмы маршрутизации, и авторы надеются, что это будет стимулировать дальнейшие теоретические события.
Полезное руководство, чтобы расширить нашу модель должно было бы рассмотреть более сложные модели трафика. Кроме того, есть потребность установить результаты конвергенции для основанных на муравье алгоритмов маршрутизации. Относительно последнего авторы ожидают, что слабой конвергенции к равновесию Wardrop (в случае алгоритма вне политики) можно показать, используя теорию стохастических алгоритмов приближения [38]. Однако, такой результат конвергенции положился бы на разделение шкалы времени между оценкой задержки и направляющий компоненты обновления алгоритма (см., например, [5], [39] и [40]), который в свою очередь драматично уменьшил бы норму, по которой алгоритм в состоянии реагировать на внезапные сетевые изменения. Таким образом, напряженность между условиями, которые гарантируют конвергенцию, и те, которые допускают быстрому ответу, являются вопросом, который заслуживает дальнейшего внимания.
Авторы хотели бы благодарить анонимные рефери за их полезные предложения в улучшении бумаги. Мы также благодарны за то, что Питер Taylor участвует нами во многих полезных обсуждениях, и для его ценного ввода к исследованию, представленному в этой газете. Andre Costa хотел бы признать поддержку австралийского Исследовательского Центра повышения спортивного мастерства Совета для Математики и Статистики Сложных Систем. Он также подтверждает получение Учености Южного австралийского Премьер-министра для Информационной технологии, и австралийского Вознаграждения Последипломного образования.
[1] D. Bertsekas и J. Gallager, Сети передачи данных, Prentice Hall, Энглвудские Утесы, Нью-Джерси (1992).
[2] R.S. Sutton и A.G. Barto, Укрепление, Учащееся: Введение, Пресс Массачуссетского технологического института, Кембридж, Массачусетс (1998).
[3] J. Boyan и М. Littman, маршрутизация Пакета в динамически изменяющихся сетях: укрепление, изучая подход, Усовершенствования в Нервном издании Систем Обработки информации 6, Morgan Kaufmann, Сан-Франциско, Калифорния (1993) стр 671–678.
[4] P. Choi и D. Yeung, Прогнозирующая Q-маршрутизация: основанное на памяти укрепление, изучая подход к адаптивному управлению транспортными потоками. В: S. Touretzky, М. Mozer и E. Hasselmo, Редакторы, Усовершенствования в Нервном издании Систем Обработки информации 8, Пресс Массачуссетского технологического института, Кембридж, Массачусетс (1996), стр 945–951.
[5] V.S. Borkar и P. Kumar, Динамическая cesaro-wardrop балансировка в сетях, ИИЭР Сделки на Автоматическом управлении 48 (2003) (3), стр 382–396. Резюме-INSPEC | Резюме-Compendex | $Order Документ | Полный Текст через CrossRef
[6] E. Bonebeau, М. Dorigo и T. Theraulaz, От Естественного до Искусственной Разведки Роя, Пресса Оксфордского университета, Нью-Йорка (1999).
[7] М. Dorigo и T. Stutzle, Оптимизация Колонии муравьев, Пресс Массачуссетского технологического института, Кембридж (2004).
[8] E. Bonebeau, F. Henaux, S. Guerin, D. Snyers, P. Kuntz и Г. Theraulaz, Направляющий в телекоммуникационных сетях с “умными подобными муравью агентами, Слушаниями IATA ’98, Второй Int. Симпозиум относительно Интеллектуальных Агентов для Телекоммуникационных Приложений, Примечаний Лекции в АЙ издании 1437, Springer, Берлин (1998).
[9] Г. Di Caro и М. Dorigo, AntNet: Распределенные stigmergetic управляют для систем коммуникаций, Журнала Исследования Искусственного интеллекта 9 (1998), стр 317–365.
[10] М. Huesse, D. Snyers, S. Guerin и P. Kuntz, Адаптивная управляемая агентом загрузка, балансирующая в сетях коммуникации, Усовершенствования в Сложных Системах 1 (1998), стр 237–254.
[11] R. Schoonderwoerd, O. Голландия, J. Bruten и L. Rothkrantz, Основанная на муравье загрузка, балансирующая в телекоммуникационных сетях, Адаптивное Поведение 5 (1996), стр 169–207. Резюме-INSPEC | $Order Документ
[12] T. Белый, B. Pagurek и F. Oppacher, управление Подключением, использующее адаптивных мобильных агентов, Слушания Международной Конференции по Параллели и Распределенным Методикам Обработки и Приложениям, Прессу CSREA (1998).
[13] K. Сим и W. Солнце, оптимизация Колонии муравьев для маршрутизации и балансирования загрузки: обзор и новые указания, ИИЭР Сделки на Системах, Человеке и Кибернетике - Часть A: Системы и Люди 33 (2003), стр 560–573.
[14] S. Томас, IP Переключающиеся и Направляющие Основные темы, Wiley, Нью-Йорк (2002).
[15] М Osborne и A. Rubenstein, Курс в Теории Игры, Прессе Массачуссетского технологического института, Кембридже, Массачусетс (1994).
[16] D. Bertsekas, Нелинейное Программирование, Athena Scientific, Belmont, Массачусетс (1999).
[17] J.G. Wardrop, Немного теоретических аспектов исследования дорожного транспорта, Proc. Учреждение Инженеров - строителей, Вторая часть 1 (1952), стр 325–362.
[18] E. Bonebeau, М. Dorigo и T. Theraulaz, Вдохновение для оптимизации от социального поведения насекомого, Природа 406 (2000), стр 39–42.
[19] J. Deneubourg, S. Aron, S. Goss и J. Pasteels, самоорганизовывающее исследовательское поведение аргентинского муравья, Журнал Поведения Насекомого 3 (1990), стр 159–168. Полный Текст через CrossRef
[20] М. Millonas, Рои, фаза, переходы и коллективная разведка, Искусственная Жизнь III, Исследования SFI в Науке Сложности, Addison-Уэсли, Чтения, Массачусетс (1994).
[21] Г. Di Caro, М. Dorigo и L. Gambardella, алгоритмы Муравья для дискретной оптимизации, Искусственная Жизнь 5 (1999), стр 137–172.
[22] A. Коста, Аналитическое Моделирование Основанной на агенте Сети, Направляющей Алгоритмы, диссертацию, Школу Прикладной Математики, Университет Аделаиды, 2003.
[23] L. Kleinrock, издание Систем Организации очередей 1, Wiley, Нью-Йорк (1975).
[24] D. Bertsekas и J. Tsitsiklis, Neuro-динамическое Программирование, Athena Scientific, Belmont, Массачусетс (1996).
[25] М. Puterman, Марковские Проблемы Решения, Wiley, Нью-Йорк (1994).
[26] N. Dunford и J. Schwartz, Линейные Операторы, Издатели Межнауки, Нью-Йорк (1958).
[27] D. Bertsekas, Динамическое Программирование и Оптимальное управление, издание. II, Athena Scientific, Belmont, Массачусетс (1995).
[28] S. Dafermos и F. Воробей, проблема назначения трафика для общей сети, Журнала Исследования Национального Бюро Стандартов 73 (1969), стр 91–118. Резюме-INSPEC | $Order Документ | MathSciNet
[29] T. Булонь, E. Altman, H. Kameda и O. Pourtallier, Смешанное равновесие для мультикласса, направляющего игры, ИИЭР Сделки на Автоматическом управлении 47 (2002), стр 913–916.
[30] Y. Korilis и A. Нищий, На существовании равновесия в несовместном оптимальном управлении потоком данных, Журнале ACM 42 (1995) (3), стр 584–613. Резюме-INSPEC | $Order Документ | MathSciNet | Полный Текст через CrossRef
[31] A. Orda, R. ПЗУ и N. Shimkin, Конкурентоспособная маршрутизация в многопользовательских системах коммуникаций, Сделках IEEE/ACM при Организации сети 1 (1993), стр 510–521. Резюме-Compendex | Резюме-INSPEC | $Order Документ | Полный Текст через CrossRef
[32] A. Haurie и P. Marcotte, На отношениях между nash-cournot и wardrop равновесием, Сети 15 (1985), стр 295–308. Резюме-INSPEC | Резюме-Compendex | $Order Документ | MathSciNet
[33] D. Bertsekas, E. Gafni и R. Gallagher, Вторые производные алгоритмы для минимальной задержки, распределенной, направляя в сетях, ИИЭР Сделки на Связи 32 (1984), стр 911–919. Резюме-INSPEC | $Order Документ | MathSciNet | Полный Текст через CrossRef
[34] D. Регент и М. Gerla, Оптимальная маршрутизация в сети коммутации пакетов, ИИЭР Сделки на Компьютерах 23 (1974), стр 1062–1068.
[35] C. Cassandras, V. Abidi и D. Towsley, Распределенная маршрутизация с сетевой крайней оценкой задержки, ИИЭР Сделки на Связи 38 (1990), стр 348–359. Резюме-INSPEC | Резюме-Compendex | $Order Документ | Полный Текст через CrossRef
[36] R. Gallagher, минимальная задержка, направляющая алгоритм, используя распределенное вычисление, ИИЭР Сделки на Связи 25 (1979), стр 73–85.
[37] D. Bertsekas, Динамическое поведение самого короткого пути, направляющего алгоритмы для сетей коммуникации, ИИЭР Сделки на Автоматическом управлении 27 (1982), стр 60–74. Резюме-INSPEC | $Order Документ | MathSciNet | Полный Текст через CrossRef
[38] H. Kushner, Стохастические Алгоритмы Приближения и Приложения, Springer, Нью-Йорк (1997).
[39] V.S. Borkar, Асинхронные стохастические приближения, СИАМСКИЙ Журнал на Управлении и Оптимизации 36 (1998) (3), стр 840–851. Резюме-Compendex | Резюме-INSPEC | $Order Документ | MathSciNet | Полный Текст через CrossRef
[40] V. Konda и J. Tsitsiklis, алгоритмы Актера-критика, СИАМСКИЙ Журнал на Управлении и Оптимизации 42 (2003) (4), стр 1143–1166. Резюме-INSPEC | $Order Документ | Полный Текст через CrossRef
Аналитическая модель, представленная в Разделе 5, может быть приспособлена, чтобы представить версию вне политики основанного на муравье алгоритма маршрутизации, который описан в Разделе 8, следующим образом.
Мы заменяем данные, направляющие матрицу Ψ (σ, n), с непараметризовавшей матрицей Ψ (n), который обновлен согласно процедуре, определенной в Разделе 8. Матрица маршрутизации Ψ (n) уникально определяет путь, которым Сицзян запросов трафика данных, направлены через сеть, таким образом приводя к потокам узла данных и потокам ссылки.
В моделировании потоков трафика муравья мы должны учесть факт, что в версии вне политики алгоритма, муравьи выполняют первое исследование перелета, и следуют за данными, направляющими политику Ψ (n), для всех последующих выборов ссылки. Предположите еще раз, что запрос трафика муравья, вводящий сеть в узел, мной дают.gif){kind=small}
. Кроме того, предположите, что муравьи выбирают свою первую ссылку перелета однородно наугад. Из этого следует, что трафик муравья, созданный в узле я, создаст скупой поток трафика k на каждой уходящей ссылке.gif){kind=small}
, и таким образом запрос трафика муравья k в каждом узле.gif){kind=small}
, который впоследствии направлен адресату согласно данным, направляющим политику. Детали представлены в [22].
Принимая во внимание измененные потоки трафика муравья, как описано выше, мы комбинируем муравья и потоки трафика данных, чтобы получить полные потоки ссылки, fij (n), которые в свою очередь дают начало ожидаемым задержкам ссылки, Rij (n). Q-значениями тогда дают
.gif){kind=small}
по условию направляя вероятности, отражая факт, что муравьи используют данные, направляющие вероятности для всех выборов ссылки, последующих за первым перелетом. Решение системы уравнений (33) может быть написано в векторной форме какОтображение, управляющее обновлениями данных, направляющих матрицу, получено в прямой манере, индексируя переменные количества в Рис. правил обновления (28), (29) и (31) использование n = 1, 2 .
После того же самого подхода как в Разделе 5, мы можем выразить аналитическую модель для алгоритма вне политики, используя более компактное примечание. Мы опускаем детали, которые являются прямыми, и даны в [22]. Кратко, мы можем создать соединение, отображающее F
, который отображает данные, направляющие вероятности к Q-значениям, и соединение, отображающее Ω, который отображает данные, направляющие вероятности и Q-значения к данным, направляющим вероятности. Аналитическая модель для алгоритма вне политики может тогда быть выражена как итерация данных, направляющих вероятности
В отличие от этого в Разделе 5, здесь не возможно выразить аналитическую модель как итерацию одних только Q-значений. Это - то, потому что в версии вне политики, данные, направляющие вероятности, непосредственно не определены Q-значениями. Определенно, отображение Ω * определяет возрастающее обновление к существующим данным, направляющим вероятности, основанные на Q-значениях, но не определяет вероятности маршрутизации непосредственно от Q-значений, также, как и отображение Ω в Разделе 5.
Соответствующий автор. Адрес: Центр повышения спортивного мастерства для Математики и Статистики Сложных Систем, Университета Мельбурна, Мельбурна 3010, Австралия. Тел.: +61 3 8344 1619; факс: +61 3 8344 4599.  |
Найджел Bean в настоящее время - Кафедра Прикладной Математики в Университете Аделаиды. Его предыдущая позиция была как Директор Математического Моделирования TRC, коммерчески финансируемого исследования и консалтинговой фирмы, которая является частью Прикладной Математики в Университете Аделаиды. Найджел - получатель 2001 J.H. Митчелл Medal, награжденный австралийцем и Новой Зеландией Индустриальная и Прикладная Математика (ANZIAM) подразделение австралийского Математического Общества, и 2003 P.A.P. Медаль Moran награждает австралийская Академия Науки. Найджел был награжден своим доктором философии Университетом Кембриджа в 1993 и контролировался Франком Kelly, FRS. |
.jpg) |
Andre Costa в настоящее время - Исследовательский Товарищ в Центре повышения спортивного мастерства для Математики и Статистики Сложных Систем в Университете Мельбурна. Его предыдущая позиция была Ассистентом в Прикладной Математике в Университете Аделаиды. Andre Costa был награжден своим доктором философии в Прикладной Математике Университетом Аделаиды в 2003, и контролировался Найджелом Bean и Питером Taylor. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Том 49, Проблема 2, 5 октября 2005, Страницы 243-268 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| Авторское право © 2005 Elsevier B.V. Все права защищены. ScienceDirect® - регистрированная торговая марка Elsevier B.V. |
(1-γ) .gif)
.gif)
.gif){kind=small}
.gif)
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif)
.gif)
.gif){kind=small}
.gif){kind=small}
.gif)
.gif)
.gif)
.gif){kind=small}
.gif)
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif)
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif)
.gif){kind=small}
.gif)
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif)
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif)
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif){kind=small}
.gif)
.gif){kind=small}